Lineární algebra 2
Cvičení k přednášce Lineární algebra 2 [NMAI058] v letním semestru 2021/2022. Probíhá v pondělí od 10:40 v učebně N3 v pavilonu IMPAKT v Tróji. Cvičení vedeme společně s Matyášem Lorencem.
Cílem cvičení je lépe pochopit pojmy a probíranou látku z přednášek, dále taktéž procvičovat teorii na počítaných příkladech a spočítat si i některé čistě aplikační úlohy.
Těm, kteří by měli zájem o trochu víc, mohu doporučit cvičení z Lineární algebry 2 pro pokročilé, které vedeme společně s Nikolou Kalábovou. V rámci cvičení se snažíme si vybudovat "vlastní matematiku", přirozeně dojít k definicím lineární algebry, případně ukázat alternativní důkazy vět k těm, jež byly představeny na přednáškách a tím více prohloubit pochopení daných tvrzení. Cvičení je možné naštěvovat i v případě, že jste již zapsání na jiné cvičení.
Požadavky na zápočet
Zápočet bude udělen za získání alespoň 50% bodů z domácích úkolů (35 ze 70 bodů), které naleznete zde (poslední update 23.1.2022). Úlohy jsou rozděleny tematicky do sérií, které mají určené deadliny. Po uplynutí deadlinu je možné za vyřešené úlohy získat polovinu bodů.
Současné body studentů
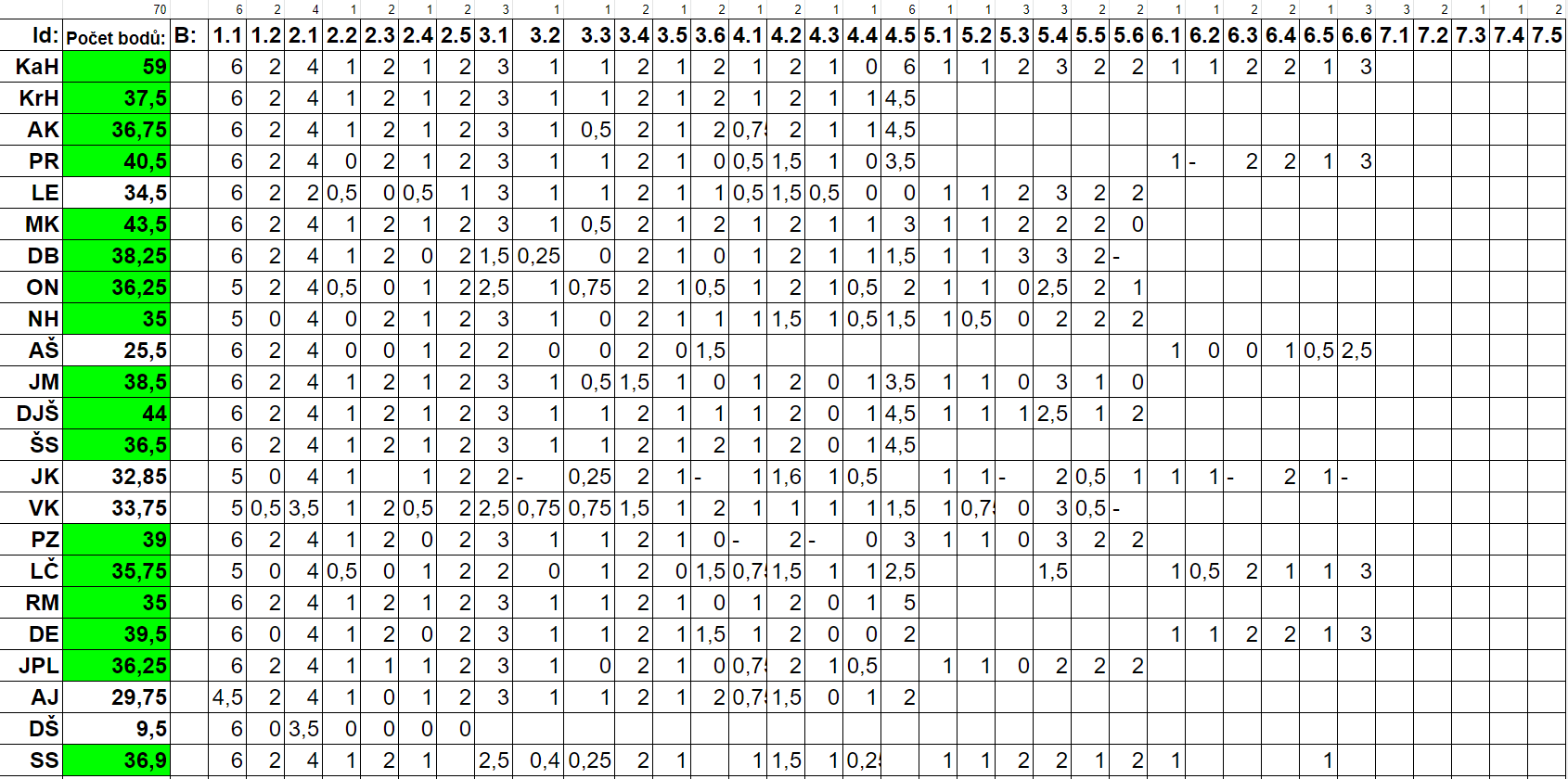
Literatura a materiály
- vzorová cvičení doc. Hladíka
- elektronická sbírka doc. Fialy
- Milan Hladík: Lineární algebra (nejen) pro informatiky, Praha 2019.
- Jindřich Bečvář: Lineární algebra, Matfyzpress, 2. vydani, Praha 2002.
- Jiří Rohn: Lineární algebra a optimalizace, Karolinum, Praha 2004.
- Ladislav Bican, Lineární algebra a geometrie. Academia, Praha 2002.
Cvičební materiály
| Probíráno: | Téma: | Zadání: | Řešení: |
|---|---|---|---|
| 14.2.2022 | Shrnutí LA2 | zde | zde |
| 19.2.2022 | Znaménko permutace a výpočet determinantu | zde | zde |
| 21.2.2022 | Determinant geometricky, adjunkce a Cramer | zde | zde |
| 28.2.-7.3.2022 | Vlastní čísla | zde | zde |
| 14.3.2022 | Diagonalizovatelnost | zde | zde |
| 14.3.2022 | Jordanova normální forma | zde | zde |
| 14.3.2022 | Markovovy řetězce a výpočet vlastních čísel | zde | zde |
| 21.3.2022 | Opakování | zde | zde |
| 28.3-4.4.2022 | Skalární součin a norma | zde | zde | 11.4.2022 | Ortogonální systém a GS ortogonalizace | zde | zde |
| 18.4.2022 | Velikonoční pondělí | zde | zde |
| 25.4.2022 | Ortogonální doplněk a projekce | zde | zde |
| 25.4.2022 | Ortogonální matice | zde | zde |
| 2.5.2022 | Positivně semi-definitní matice | zde | zde |
| 2.5.2022 | Choleského rozklad | zde | zde |
| 9.5.2022 | Bilineární a kvadratické formy | zde | zde |
| 9.5.2022 | Sylvestrův zákon setrvačnosti | zde | zde |
| 16.5.2022 | Opakování |