Lineární algebra 2
Pokročilá cvičení k přednášce Lineární algebra 2 [NMAI058] v letním semestru 2021/2022. Probíhá v pondělí od 9:00 v učebně N3 v pavilonu IMPAKT v Tróji. Cvičení vedeme společně s Nikolou Kalábovou (niki@kam.mff.cuni.cz).
Na cvičení se pokusíme si vybudovat "vlastní matematiku". Pokusíme se přirozeně přijít k definicím, místo toho, aby nám "spadly z nebe". Ukážeme si alternativní důkazy k větám, které byly představeny na přednášce, abychom hlouběji a z jiného úhlů pochopily, co vlastně tvrdí. V neposlední řadě čas od času i zmíníme věci, které se na přednáškách nestihly včetně aplikací lineární algebry.
Cvičení bude z části vycházet z následujícího textu.
Pro účast na cvičení není potřeba žádných předchozích znalostí nad rámec základního kurzu lineární algebry 1. Cvičení je možné absolvovat i v případě, že máte již zapsané jiné cvičení.
Požadavky na zápočet
Zápočet bude udělen za získání alespoň 100 bodů z domácích úkolů.
Vypsané jsou úlohy za dohromady 150 bodů (zde) + dalších až 160 bodů lze získat za vyřešení úloh z těch, které byly vypsány v zimním semestru a o jejich řešení jste se ještě nepokusili (zde).
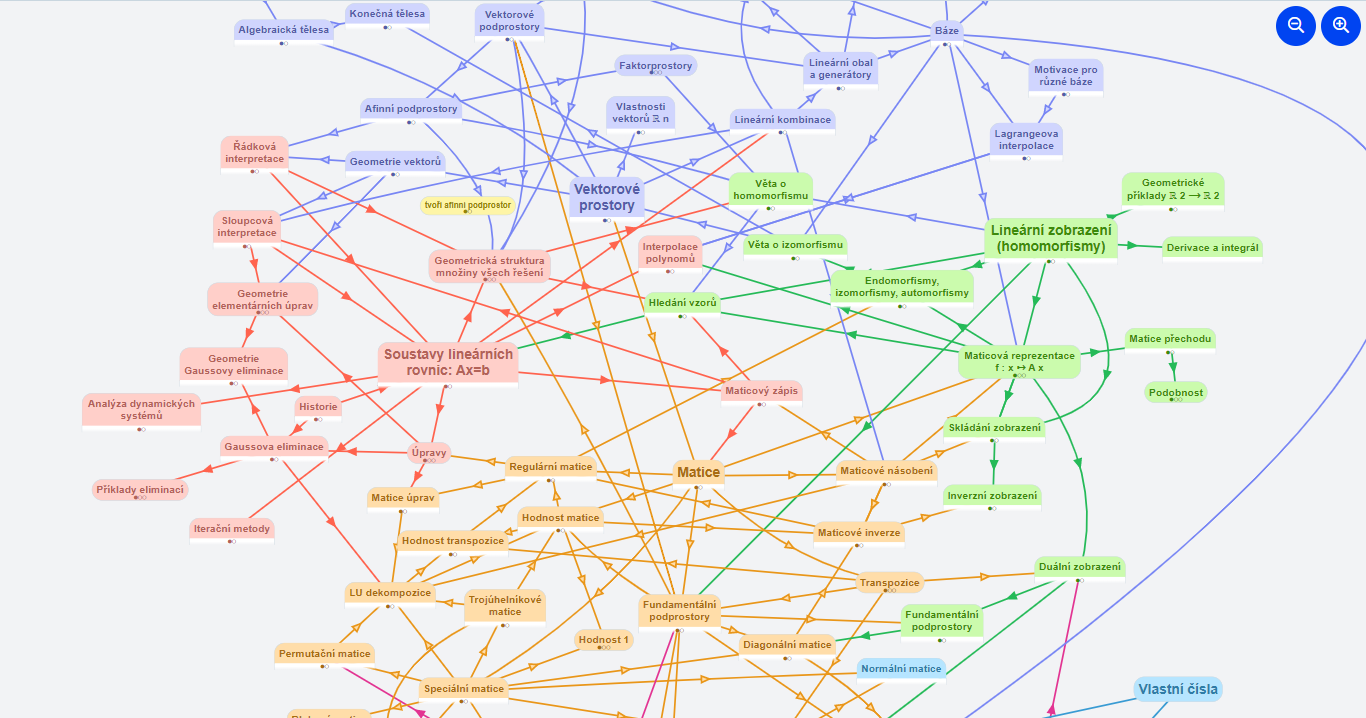
Alternativně lze získat zápočet za vytvoření strukturálního diagramu pro lineární algebru nebo obecně matematiku v nástroji Orgpad (příklad diagramu a návod používání). Cílem je vytvořit si nad lineární algebrou strukturu ve vlastní hlavě, zařadit si pojmy, uvědomit si jejich závislosti. Zároveň může sloužit tvorba diagramu jako dobrá příprava na ústní část zkoušky. Na první pohled se může zdát, že se jedná o ohromné množství práce, ale pokud student na diagramu pracuje v průběhu semestru (například po shlédnutí přednášky si rozmyslí a zapíše, co se dozvěděl), tak časová náročnost není velká. V případě zájmu napište některému ze cvičících mail. Ideální je práci na svém diagramu v průběhu semestru několikrát konzultovat.
Ukázka strukturálního diagramu v nástroji Orgpad:
Seznam cvičení
| Datum | Popis cvičení | Prezentace |
|---|---|---|
| 14.-21.2.2022 | Standardní skalární součin a norma | zde |
| 21.-28.2.2022 | Abstraktní definice skalárního součinu a normy | zde |
| 7.-14.3.2022 | Ortogonální projekce a Cauchy-Schwarzova nerovnost | zde |
| 14.-21.3.2022 | Ortogonální báze a Gram-Schmidtova ortogonalizace | zde |
| 21.3.2022 | Metoda nejmenších čtverců | zde |
| 28.3.2022 | Determinanty a jejich vlastnosti | zde |
| 4.-11.4.2022 | Vlastní čísla | zde |
| 18.4.2022 | Velikonoční pondělí | zde |
| 25.4-2.5.2022 | Diagonalizace, vlastní čísla a Gerschgorinovy disky | zde |
| 2.5.2022 | Schurův a spektrální rozklad | zde |
| 9.5.2022 | Pozitivně definitní matice: extrémy a energie | zde |
| 16.5.2022 | Sylvestrova věta o setrvačnosti a minimaxová věta | zde |