On this webpage you can find examples of broader topics from discrete geometry an combinatorics. If you are interested in some of them, please contact me (by e-mail) and we will discuss a more detailed specification. We can also agree on a different topic from the area.
For most of the topics it may be useful to write a program for investigating or visualization of small cases; a credit for a software project can be given for an implementation of reasonable quality.
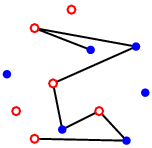Is it possible to draw a given graph in the plane so that the set of its vertices forms a given point set, and the edges are drawn as straight-line segments without crossing? What if the points and vertices are colored and the colors of points and vertices have to match? What if we want the drawing to exist for any coloring of the points or vertices? How many more points do we need for the drawing to exist? What if instead of coloring we orient the edges and require them to point upwards?
As particular example, we may consider a path with vertices colored alternately red and blue. Even for points in convex position it is not known how many points are needed to draw such an alternating red-blue path. The core of this problem is a combinatorial problem of finding a longest common subsequence in two zero-one sequences where the density of ones and zeros is almost the same.
Euclidean Ramsey theory is concerned with questions of the following type: a configuration T consisting of finitely many points in the plane or in R^d is given; for example, the set of vertices of a triangle or a square. Given n ≥ d and k, does every coloring of R^n with k colors contain a monochromatic copy of T? Many variants of the problem can be studied, for example special types of colorings, or searching for different configurations in different colors.
The Hadwiger–Nelson problem about the so-called chromatic number of the plane is perhaps the most famous problem of this type. A breakthrough result from the beginning of 2018, improving the lower bound from 4 to 5, was achieved by an amateur mathematician, otherwise known as the leading expert on the problem of aging. Shortly after, a polymath project was created, aimed at improving the result further. Some of the methods might be applied also for solving other related questions.
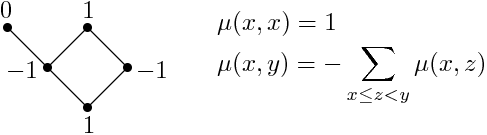The Möbius function of a poset is a useful tool for enumerating combinatorial objects. It can be computed either from a simple recursive formula or directly as the difference between the numbers of even and odd chains. From the values of the Möbius function of the inclusion poset one can derive the classical inclusion-exclusion principle. Möbius function is also an equivalent form of Euler characteristic, an important invariant of geometric and topological objects arising in different fields of mathematics.
In combinatorics, the Möbius function was investigated for example for the posets of words or permutations. It would be interesting to try to achieve similar results in other combinatorial posets, for example defined in terms of permutations or graphs.
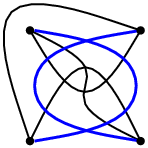The genus of a graph G is the smallest genus ("number of holes") of an orientable surface where G can be drawn without crossings. The Z2-genus of G is the smallest genus of an orientable surface where G can be drawn so that edges with no common vertex cross an even number of times. By the Hanani–Tutte theorem, every graph of Z2-genus 0 is planar, that is, it has genus 0. It was an open question whether a generalization of this theorem, according to which a graph of Z2-genus g would also have genus g, is true. Recently, with R. Fulek, we found a counterexample on a surface of genus 4. This makes determining the Z2-genus of various graphs an interesting problem.
The goal of the project would be implementing an algorithm for computing the Z2-genus of a graph, perhaps also the genus or other similar parameters. From the theoretical perspective it would be interesting to find small graphs whose Z2-genus and genus differ, improve bounds on the Z2-genus of some classes of graphs, investigate similar questions on nonorientable surfaces etc. The topic will involve some linear-algebraic coputation over the two-element field.
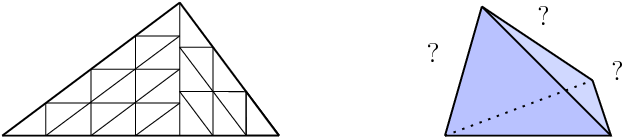A polytope P (or a more general subset of R^d) that can be tiled with k congruent tiles similar to P, is called a k-reptile. Many examples of k-reptile polytopes and
sets are known, but not much about their characterization is known, even in the case of simplest polytopes, simplices. It would be interesting to find new examples of k-reptile simplices, or prove that for certain values of k such simplices do not exist. Linear-algebraic knowledge and skills might be useful.
The problem of the existence of k-reptile simplices was originally motivated by probabilistic marking of IP packets to identify their source.
A polycube is a polytope composed from unit cubes arranged in the cubical lattice; in addition we assume that it has no airtight cavities. The surface of a polycube is then a connected union of unit squares. Is it possible to cut the surface of a given polycube along the grid lines and unfold to the plane, so that no two squares overlap? In other words, can every polycube be cut and folded from a square paper?
This question is still open, but partial solutions for special types of polycubes are known. The goal of the project would be implementing some selected unfolding algorithms. The goal of the theoretical part would be extending the known results to some new types of polycubes.
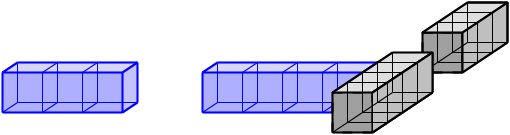In 2016, Gruslys, Leader a Tan showed that, every finite subset of the integer lattice Z^d tiles a lattice Z^n of a sufficiently large dimension. One could also say that every (even disconnected) polycube tiles a Euclidean space of a sufficiently large dimension. The estimated dimension is rather huge. For some special type of tiles, tilings in fewer dimensions are known. The case of one-dimensional tiles - subsets of Z - is already interesting and far from solved. For example, it can be shown that the disconnected tile "XX.XX" tiles Z^2, or that "XXX.XXX" tiles Z^3.
The goal of the project would be implementing a program for finding periodic tilings; in other words, tilings of a higher-dimensional torus of suitable size. The goal of the theoretical part would be extending the known results and finding tilings of low-dimensional spaces by more types of tiles.
Handbook of discrete and computational geometry, Third edition, Edited by Jacob E. Goodman, Joseph O'Rourke and Csaba D. Tóth, Discrete Mathematics and its Applications (Boca Raton), CRC Press, Boca Raton, FL, 2018, ISBN: 978-1-4987-1139-5. Electronic version: http://www.csun.edu/~ctoth/Handbook/HDCG3.html