Na této stránce jsou uvedeny příklady širších témat z diskrétní geometrie a kombinatoriky; pokud Vás nějaké zaujme, kontaktujte mě např. e-mailem a pokusíme se dohodnout na konkrétním zadání. Můžeme se dohodnout i na jiném tématu z oblasti.
U většiny témat může být velmi vhodné napsat si program na zkoumání nebo vizualizaci malých případů; kvalitní implementaci je možné pojmout jako ročníkový projekt. Konkrétní zadání bude záviset na dohodnutém tématu.
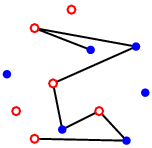 Je možné daný graf nakreslit v rovině tak, aby jeho vrcholy tvořily zadanou množinu bodů, hrany byly nakreslené jako úsečky, a přitom se nekřížily? Co když jsou navíc body v rovině i vrcholy grafu obarvené červeně a modře, a každý vrchol musí být nakreslen na bod své barvy? Co když navíc chceme, aby takové nakreslení existovalo pro každé kompatibilní obarvení zadaných bodů nebo vrcholů? O kolik víc bodů je potřeba, aby šel graf popsaným způsobem nakreslit? Místo obarvování bodů a vrcholů je také možné např. zorientovat hrany grafu a požadovat, aby při nakreslení všechny hrany směřovaly vzhůru.
Je možné daný graf nakreslit v rovině tak, aby jeho vrcholy tvořily zadanou množinu bodů, hrany byly nakreslené jako úsečky, a přitom se nekřížily? Co když jsou navíc body v rovině i vrcholy grafu obarvené červeně a modře, a každý vrchol musí být nakreslen na bod své barvy? Co když navíc chceme, aby takové nakreslení existovalo pro každé kompatibilní obarvení zadaných bodů nebo vrcholů? O kolik víc bodů je potřeba, aby šel graf popsaným způsobem nakreslit? Místo obarvování bodů a vrcholů je také možné např. zorientovat hrany grafu a požadovat, aby při nakreslení všechny hrany směřovaly vzhůru.
Konkrétním problémem je např. případ cesty, jejíž vrcholy jsou střídavě obarveny červeně a modře. I když se omezíme na množiny bodů v konvexní poloze, není známé, jaký minimální počet bodů na nakreslení takové červeno-modré cesty stačí. Jádro tohoto problému tvoří kombinatorický problém hledání nejdelší společné podposloupnosti ve dvou posloupnostech nul a jedniček, kde se obě číslice vyskytují přibližně se stejnou frekvencí.
 Euklidovská ramseyovská teorie se zabývá otázkami následujícího typu: je zadána konfigurace T sestávající z konečně mnoha bodů v rovině nebo v R^d; například množina vrcholů trojúhelníka nebo čtverce. Lze pak v každém obarvení prostoru R^n pomocí k barev najít jednobarevnou kopii T? Dají se zkoumat různé varianty problému, např. pro speciální typy obarvení, nebo hledat v různých barvách různé konfigurace.
Euklidovská ramseyovská teorie se zabývá otázkami následujícího typu: je zadána konfigurace T sestávající z konečně mnoha bodů v rovině nebo v R^d; například množina vrcholů trojúhelníka nebo čtverce. Lze pak v každém obarvení prostoru R^n pomocí k barev najít jednobarevnou kopii T? Dají se zkoumat různé varianty problému, např. pro speciální typy obarvení, nebo hledat v různých barvách různé konfigurace.
Do této oblasti spadá i slavný Hadwigerův–Nelsonův problém o určení tzv. chromatického čísla roviny. Průlomového výsledku, vylepšujícího dolní odhad ze 4 na 5, se podařilo začátkem roku 2018, po více než 60 letech, docílit amatérskému matematikovi, který je jinak předním expertem na problém stárnutí. Následovalo založení polymath projektu zaměřeného na další vylepšování výsledku. Některé z navržených metod by mohly nalézt uplatnění i při řešení ostatních otázek.
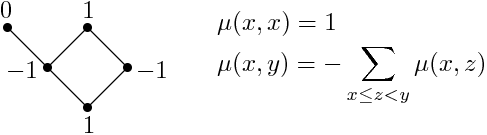 Möbiova funkce pro částečně uspořádané množiny (posety) je užitečným nástrojem při počítání kombinatorických objektů. Lze ji spočítat buď pomocí jednoduché rekurzivní formule nebo přímočaře jako rozdíl počtu sudých a lichých řetězců. Z hodnot Möbiovy funkce pro uspořádání podmnožin inkluzí lze např. odvodit klasický princip inkluze a exkluze. Möbiova funkce je také ekvivalentním vyjádřením Eulerovy charakteristiky, což je významný invariant geometrických a topologických objektů objevující se v různých oborech matematiky.
Möbiova funkce pro částečně uspořádané množiny (posety) je užitečným nástrojem při počítání kombinatorických objektů. Lze ji spočítat buď pomocí jednoduché rekurzivní formule nebo přímočaře jako rozdíl počtu sudých a lichých řetězců. Z hodnot Möbiovy funkce pro uspořádání podmnožin inkluzí lze např. odvodit klasický princip inkluze a exkluze. Möbiova funkce je také ekvivalentním vyjádřením Eulerovy charakteristiky, což je významný invariant geometrických a topologických objektů objevující se v různých oborech matematiky.
V kombinatorice byla Möbiova funkce počítána např. pro částečná uspořádání slov nebo permutací. Bylo by zajímavé pokusit se o podobné výsledky v dalších kombinatorických uspořádáních, definovaných např. pomocí permutací nebo grafů.
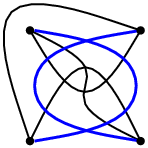 Rod grafu G je nejmenší rod ("počet děr") orientovatelné plochy, na kterou jde G nakreslit bez křížení. Z2-rod grafu G je nejmenší rod orientovatelné plochy, na kterou jde G nakreslit tak, že hrany bez společného vrcholu mají sudý počet křížení. Podle Hanani–Tutteovy věty každý graf Z2-rodu 0 je rovinný, tj. má rod 0. Na zobecnění, podle kterého by graf Z2-rodu g měl také rod g, jsme nedávno s R. Fulkem nalezli protipříklad na ploše rodu 4. Tím se určování Z2-rodu různých grafů stává zajímavým problémem.
Rod grafu G je nejmenší rod ("počet děr") orientovatelné plochy, na kterou jde G nakreslit bez křížení. Z2-rod grafu G je nejmenší rod orientovatelné plochy, na kterou jde G nakreslit tak, že hrany bez společného vrcholu mají sudý počet křížení. Podle Hanani–Tutteovy věty každý graf Z2-rodu 0 je rovinný, tj. má rod 0. Na zobecnění, podle kterého by graf Z2-rodu g měl také rod g, jsme nedávno s R. Fulkem nalezli protipříklad na ploše rodu 4. Tím se určování Z2-rodu různých grafů stává zajímavým problémem.
Úkolem projektu by bylo implementovat algoritmus na výpočet Z2-rodu grafu, případně rodu i dalších podobných parametrů. Z teoretického hlediska by bylo zajímavé najít co nejmenší konkrétní grafy, jejichž Z2-rod a rod se liší, zlepšit odhady na Z2-rod pro některé třídy grafů, zkoumat podobné otázky na neorientovatelných plochách apod. Při řešení se uplatní lineárně-algebraické výpočty nad dvojprvkovým tělesem.
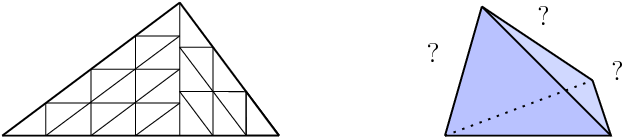 Těleso T (nebo obecnější podmnožina R^d), které jde vydláždit k shodnými dlaždicemi podobnými T, se nazývá k-reptile. Jsou známy mnohé příklady k-reptile těles a množin, ale o jejich charakterizaci se mnoho neví, a to i v případě nejjednodušších těles, simplexů. Bylo by zajímavé nalézt nové příklady k-reptile simplexů, ale i dokázat, že pro určité hodnoty k takové simplexy neexistují. Mohou se zde uplatnit znalosti z lineární algebry.
Těleso T (nebo obecnější podmnožina R^d), které jde vydláždit k shodnými dlaždicemi podobnými T, se nazývá k-reptile. Jsou známy mnohé příklady k-reptile těles a množin, ale o jejich charakterizaci se mnoho neví, a to i v případě nejjednodušších těles, simplexů. Bylo by zajímavé nalézt nové příklady k-reptile simplexů, ale i dokázat, že pro určité hodnoty k takové simplexy neexistují. Mohou se zde uplatnit znalosti z lineární algebry.
Problém existence k-reptile simplexů byl původně motivován pravděpodobnostím značkováním IP paketů za účelem identifikace jejich zdroje.
 Kostičkový mnohostěn je těleso složené z jednotkových krychlí v krychlové mřížce; předpokládáme navíc, že neobsahuje žádné vzduchotěsné dutiny. Jeho povrch je pak souvislým sjednocením jednotkových čtverců. Lze povrch každého kostičkového mnohostěnu rozřezat podél hran mřížky a rozvinout do roviny, aby se žádné dva čtverce nepřekrývaly? Jinými slovy, lze zadaný kostičkový mnohostěn vystřihnout a složit z čtverečkovaného papíru?
Kostičkový mnohostěn je těleso složené z jednotkových krychlí v krychlové mřížce; předpokládáme navíc, že neobsahuje žádné vzduchotěsné dutiny. Jeho povrch je pak souvislým sjednocením jednotkových čtverců. Lze povrch každého kostičkového mnohostěnu rozřezat podél hran mřížky a rozvinout do roviny, aby se žádné dva čtverce nepřekrývaly? Jinými slovy, lze zadaný kostičkový mnohostěn vystřihnout a složit z čtverečkovaného papíru?
Tato otázka je obecně stále otevřená, ale jsou známá částečná řešení pro speciální typy mnohostěnů. Úkolem projektu by bylo některé vybrané postupy rozkládání implementovat. Úkolem teoretické části by bylo pokusit se známé výsledky rozšířit a navrhnout rozklady pro nové typy mnohostěnů.
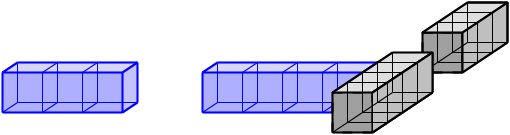 Gruslys, Leader a Tan v r. 2016 ukázali, že každou konečnou podmnožinou celočíselné mřížky Z^d lze vydláždit dostatečně-rozměrnou mřížku Z^n. Lze si to představit i tak, že každým (i nesouvislým) krychličkovým tělěsem lze vydláždit dostatečně-rozměrný euklidovský prostor. Odhady na potřebnou dimenzi jsou ale obrovské. Pro určité speciální typy dlaždic jsou známá dláždění i v méně rozměrech. Zajímavým a dosud nedořešeným případem jsou už jednorozměrné dlaždice - podmnožiny Z. Např. lze ukázat, že nesouvislá dlaždice "XX.XX" dláždí Z^2, nebo že "XXX.XXX" dláždí Z^3.
Gruslys, Leader a Tan v r. 2016 ukázali, že každou konečnou podmnožinou celočíselné mřížky Z^d lze vydláždit dostatečně-rozměrnou mřížku Z^n. Lze si to představit i tak, že každým (i nesouvislým) krychličkovým tělěsem lze vydláždit dostatečně-rozměrný euklidovský prostor. Odhady na potřebnou dimenzi jsou ale obrovské. Pro určité speciální typy dlaždic jsou známá dláždění i v méně rozměrech. Zajímavým a dosud nedořešeným případem jsou už jednorozměrné dlaždice - podmnožiny Z. Např. lze ukázat, že nesouvislá dlaždice "XX.XX" dláždí Z^2, nebo že "XXX.XXX" dláždí Z^3.
Úkolem projektu by bylo implementovat program na hledání periodických dláždění; jinými slovy, dláždění vícerozměrného torusu vhodných rozměrů. Úkolem teoretické části by bylo pokusit se nalézt dláždění prostorů nízké dimenze dalšími typy dlaždic.
Handbook of discrete and computational geometry, Third edition, Edited by Jacob E. Goodman, Joseph O'Rourke and Csaba D. Tóth, Discrete Mathematics and its Applications (Boca Raton), CRC Press, Boca Raton, FL, 2018, ISBN: 978-1-4987-1139-5. Electronic version: http://www.csun.edu/~ctoth/Handbook/HDCG3.html