Příští týden se cvičení nekoná, je děkanský sportovní den.

Catalanova čísla

Catalanovské objekty

Určete počet:

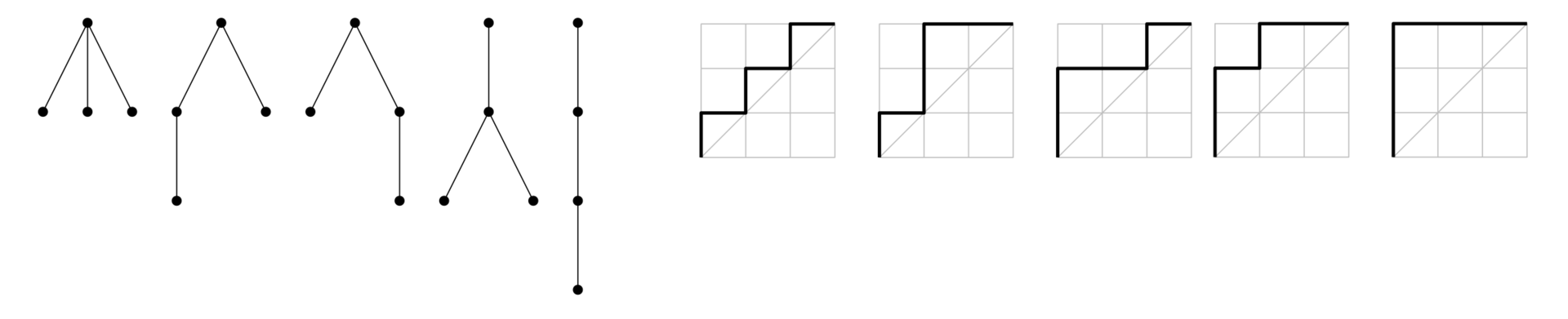
1. Zakořeněných stromů s $n$ hranami, kde každý vrchol může mít libovolný počet potomků, a potomci daného vrcholu mají určené pořadí zleva doprava. (Příklad pro $n = 3$ je v levé části obrázku.)
2. Procházky v mřížce $\N \times \N$ z bodu $(0, 0)$ do bodu $(n, n)$ takové, že v každém kroku se posuneme buď o jednu jednotku nahoru nebo o jednu jednotku doprava, a zároveň nesmíme nikdy sestoupit pod přímku danou rovnicí $x = y$. (Příklad pro $n = 3$ je v pravé části obrázku.)

Každou z předešlých úloh můžete ukázat:

1. buď pomocí rekurzivního vzorečku,
2. nebo pomocí bijekce na jiné objekty, jejichž počet už znáte.

Alternativní odvození vzorečku pro $C_n$

Vyřešme část b) předchozího příkladu kombinatorickou úvahou. V tomto příkladu slovem procházka označme libovolnou cestu v $\N \times \N$ , která začíná v bodě $(0, 0)$ a v každém kroku se posune o jedna doprava nebo o jedna nahoru. Řekneme, že procházka je dobrá, pokud nikdy nesestoupí pod přímku $x = y$, jinak je špatná.

1. Kolik existuje všech procházek (dobrých i špatných) končících v bodě $(m, n) \in \N \times \N$?
2. Dokažte pomocí vhodné bijekce, že počet všech procházek končících v bodě $(n + 1, n - 1)$ je stejný, jako počet špatných procházek končících v bodě $(n, n)$.
3. Odvoďte z toho, že počet dobrých procházek končících v bodě $(n, n)$ je ${1\over n+1}{2n \choose n}$.

Projektivní roviny

Alternativní axiomatizace

Ukažte, že axiom 3 lze nahradit axiomem: Existují dvě různé přímky $p, q$ z $\cal P$, z nichž každá obsahuje alespoň tři různé body.

Konstrukce

Nechť $p$ je prvočíslo a $[p] = \{0,1,\dots, p-1\}$. Uvažme množinu trojic $[p]^3-\{(0,0,0)\}$. Na této množině zavedeme ekvivalenci $(x_1, y_1, z_1) \sim (x_2, y_2, z_2)$ právě tehdy když existuje $\alpha \in \{1,2,\dots, p-1\}$ takové, že: $$x_1 \equiv \alpha \cdot x_2 \qquad y_1 \equiv \alpha \cdot y_2 \qquad z_1 \equiv \alpha \cdot z_2 \qquad ({\rm mod}\ p).$$ Množinu všech tříd ekvivalence $\sim$ ozmačíme $X$.

Definujeme ${\cal P} = \{\{(x,y,z) \mid (x,y,z)\in [p]^3, ax+by+cz \equiv 0 \ ({\rm mod}\ p) \} \mid (a,b,c)\in [p]^3-\{(0,0,0)\}\}$.

1. Ověřte, že $\sim$ je skutečně relace ekivalence.
2. Ověřte, že $(X, {\cal P})$ je projektivní rovina. Nejprve nahlédněte, že vnitřní množina v definici ${\cal P}$ se skládá vždy z celých tříd ekivalence $\sim$. Dále si rozyslete, že pro různá $a,b,c$ ze stejne třídy ekvivalence $\sim$ dosteneme stejnou množinu bodů (tedy pro jednu třídu ekvivalence máme jen jednu přímku). Nakonec ověřte axiomy projektivní roviny.

Nekonečné projektivní roviny

1. Nechť $X$ je množina všech (euklidovských) přímek v $\R^3$ procházejících počátkem. Pro takovou přímku $x \in X$ definujme množinu přímek $P_{\perp x} = {y \in X; y \perp x}$ a označme ${\cal P} = \{P_{\perp x} \mid x \in X\}$ systém všech takovýchto množin. Dokažte, že $(X, {\cal P})$ je projektivní rovina.
2. Nahlédněte, že tato konstrukce je ekvivalentní s následují konstrukcí: Vezmeme rovinu $\R^2$ s jejími body a přímkami. K nim doplníme pro každou množinu rovnoběžných přímek jeden bod „v nekonečnu“, kde se protínají. A pak všemi body v nekonečnu protáhneme ještě jednu přímku.