Definice. Eulerovský tah je tah v grafu, který obsahuje každou hranu grafu právě jednou.
Definice. Graf je Eulerovský, právě když v něm existuje uzavřený eulerovský tah.
Věta. Graf je eulerovský, právě když má po odstranění izolovaných vrcholů nejvýše jednu komponentu a všechny vrcholy mají sudý stupeň.
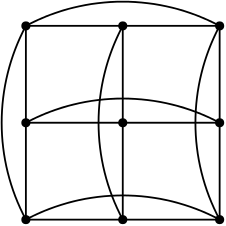
Příklad 1. U následujících grafů rozhodněte, zda jsou eulerovské:

Příklad 2. Dokažte, že každý eulerovský graf lze rozložit na hranově disjunktní sjednocení kružnic (tj. rozložit na kružnice tak, že žádné dvě nesdílí hrany).
Příklad 3. (hvězdičkový) $k$-regulární graf je graf, jehož všechny vrcholy mají stupeň $k$. Dokažte, že každý $2k$-regulární graf, lze rozložit na hranově disjunktní sjednocení dvou $k$-regulárních grafů, právě když je jeho počet vrcholů v každé komponentě souvislosti nebo $k$ sudé.
Příklad 4. Dokažte, že graf se všemi stupni sudými neobsahuje most, tedy hranu, jejíž odebrání zvýší počet komponent souvislosti.
Příklad 5. Hranový graf grafu $G(V,E)$, který má alespoň jednu hranu, je graf $L(G)(E,E')$ tak, že $\{e_1e_2\} \in E' \Leftrightarrow e_1\cap e_2\neq \emptyset$, tedy vrcholy jsou původní hrany a hrany spojují vrcholy reprezentující hrany, co měly společný vrchol. Dokažte, že hranový graf eulerovského grafu je eulerovský.
Definice. Mějme graf $G(V,E)$ a přirozené číslo $k$. $G^k$ budeme značit graf $G'$ na vrcholech $V$ takový, že $u$ a $v$ jsou spojeny hranou, pokud je vzdálenost $u$ a $v$ nejvýše $k$.
Definice. Hamiltonovská kružnice grafu $G$ je kružnice, která je podgrafem tohoto grafu, a prochází přes všechny jeho vrcholy.
Tvrzení. Rozhodnout, zda má daný graf Hamiltonovskou kružnici je NP-těžké (to znamená, není znám algoritmus, který by to dokázal v polynomiálním čase a obecně se má za to, že takový algoritmus neexistuje. Kdyby však takový algoritmus existoval, uměli bychom pomocí něj vyřešit spoustu jiných problémů).
Příklad 6. Dokažte, že pro každý strom $G$ má $G^3$ Hamiltonovskou kružnici. Najděte graf $H$ takový, že $H^2$ Hamiltonovskou kružnici mít nebude.
Příklad 7. (hvězdičkový) Na šachovnici $n\times n$ je označeno $2n$ políček. Dokažte, že na ni jde umístit šachovou věž tak, aby se donekonečna mohla pohybovat pouze po označených polích tak, že střídá vertikální a horizontální pohyby.