Definice. Řekneme, že $G(V,E)$ je izomorfní $H(V',E')$ právě když existuje $f:V\rightarrow V'$: $f$ je bijekce a pro každé $u,w \in V$ platí $(u,w)\in E$ právě když $(f(u),f(w))\in E'.$
Definice. Řekneme, že $G(V,E)$ je podgraf grafu $H(V',E')$, pokud $V\subseteq V'$ a $E \subseteq E'$ (a $G$ je stále graf, tedy $E$ nemůže obsahovat hrany k vrcholům, které nejsou v $V$).
Definice. Řekneme, že $G(V,E)$ je indukovaný podgraf grafu $H(V',E')$, pokud je to podgraf a současně "obsahuje všechny hrany které může", neboli $E=\{(u,v)\mid(u,v)\in E' \wedge u\in V \wedge v\in V\}$.
Definice. Řekneme, že $G(V,E)$ je souvislý, pokud mezi libovolnými dvěma jeho vrcholy existuje cesta.
Definice. Řekneme, že $G(V,E)$ je strom, pokud je souvislý a současně neobsahuje kružnici jako podgraf.
Příklad 1. U následujících tří grafů rozhodněte, zda je nějaká dvojice izomorfní:
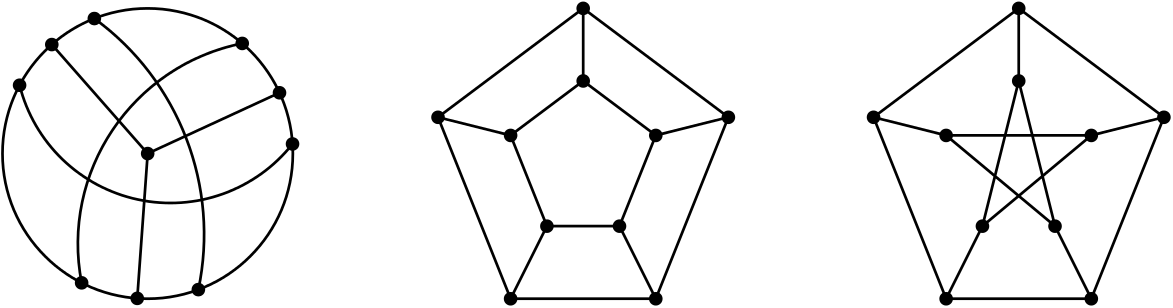
Příklad 2. Dokažte, že pokud graf obsahuje lichou kružnici jako podgraf, obsahuje lichou kružnici i jako indukovaný podgraf.
Příklad 3. Mějme graf $G(V,E)$. Dokažte, že tento graf má (ne nutně indukovaný) podgraf $G'$, který je bipartitní, ale má alespoň $\left\lceil\frac {|E|}2 \right\rceil$ hran.
Příklad 4. Rozhodněte, zda existuje graf, jehož skóre je
Příklad 5. Najděte nejmenší možný příklad (s co nejmenším počtem vrcholů) dvou souvislých neizomorfních grafů se stejným skóre.
Příklad 6. Zkuste navrhnout algoritmus, který zkontroluje, zda je daná posloupnost čísel skóre nějakého grafu v lineárním čase vzhledem k počtu vrcholů a hran.
Varování: Rozmyslete si, že nejpřímočařejší způsob implementace selže a nejpřímočařejší způsob, jak toto selhání napravit, vede na příliš pomalý algoritmus.
Příklad 7. Mějme graf, o němž platí, že mezi každými dvěma vrcholy téhož stupně vede právě jedna cesta. Je tento graf už nutně strom?
Příklad 8. (hvězdičkový) Charakterizujte množinu všech grafů, v nichž mezi každými dvěma vrcholy téhož stupně vede právě jedna cesta.
Příklad 9. Mějme strom $G$ na alespoň dvou vrcholech a jebo vrchol $v$. Dokažte, že $G$ má alespoň $deg(v)$ listů.
Příklad 10. Mějme strom $G(V,E)$ a nějaký jeho automorfismus $f$. Dokažte, že buď existuje vrchol $v$ takový, že $f(v)=v$, nebo dva vrcholy $u$, $v$ takové, že $f(u)=v$ a $f(v)=u$.