Toky, cesty a řezy (2013/14)
Minulé přednášky
3.10.2013
Multikomoditní toky a řezy - úvod, definice problémů, ILP formulace.
10.10.2013
Minimální řez - aproximační algoritmus "Potrubní řez".
17.10.2013
Dokončení analýzy algoritmu. Přibližná dualita a její meze (nejde to lépe v obecnosti).
Nejřidší řez - LP formulace.
24.10.2013
Nejřidší řez - aproximace pomocí algoritmu na minimální řez.
Algoritmus na nejřidší řez pomocí vnořování metrik - úvod, řešení LP jako metrika.
Řešení indukované vnořením.
31.10.2013
Algoritmus na nejřidší řez pomocí vnořování metrik - pokračování. Frechetovo vnoření
metriky dané řešením LP do R^d s L_1 normou. Nalezení řezu.
7.11.2013
Algoritmus na nejřidší řez pomocí vnořování metrik - pokračování. Analýza.
Důsledek 1: přibližná dualita pro spravedlivý tok a nejřidší řez.
Důsledek 2: obecný výsledek o vnořování metrik.
14.11.2013
Toky a řezy s omezenou délkou - úvod, definice. ILP formulace, úvahy
o dualitě, integrality gap - dolní odhad. Domácí úkol: kombinatorický algoritmus
pro výpočet maximálního L-omezeného toku.
21.11.2013
Vsuvka: dolní odhad na mezeru v přibližné dualitě spravedlivého toku
a nejřidšího řezu.
Horní odhad na velikost max. toku mezi s a t parametrizovany vzdalenosti
s a t. Horní odhad na integrality gap ILP pro min. L-omezený řez.
Různé O(n^{2/3})-aproximační algoritmy pro L-omezený řez.
Tokové číslo - úvod.
28.11.2013
Tokové číslo grafu - definice, smysl, výpočet. Vyvážené (balancované) instance
multikomoditních tokových problémů. Lemma o řešení vyvážených instancí
parametrizované tokovým číslem (volně: existuje "dobré a krátké" řešení).
Vztah expanze grafu a tokového čísla (bez důkazu). Zkracovací lemma: každý
přípustný tok lze nahradit jiným, skoro stejně velkým, který používá pouze
"krátké" cesty.
5.12.2013
Problém hledání maximálního počtu hranově disjunktních cest. (Ne)souvislost
s maximálním multikomoditním tokem. Aproximace pomocí hladového algoritmu
(parametrizace počtem hran, počtem vrcholů, tokovým číslem). Integrality
gap přirozené LP formulace problému.
12.12.2013
Výpočet maximálního multikomoditního toku - aproximační algoritmy založené
na Lagrangově relaxaci.
19.12.2013
Lagrangova relaxace pro max. tok - dokončení. Modifikace pro spravedlivé toky.
Výpočet maximálního multikomoditního toku - metoda generování sloupců.
2.1.2014
Semidefinitní relaxace nejmenšího balancovaného řezu. Poznamky z prednasky v ak. roce
2005/06.
9.1.2014
O(log n) aproximace nejmensiho balancovaneho rezu pomoci SDP relaxace.
Anotace
Toky více komodit zobecňují přirozeným způsobem klasický tokový problém: místo
jediné dvojice zdroj-spotřebič máme takových dvojic několik, ale přitom máme k
dispozici stále jen jedinou siť, do které se musí všechny toky poskládat. Toky
více komodit a zejména jejich duální řezové problémy hrály v posledním
desetiletí významnou úlohu při návrhu aproximačních algoritmů pro celou radu
rozmanitých aplikací, např. pro vyvážené dělení grafu či pro aproximaci
expanze grafu. Cílem přednášky je představit vybrané výsledky z této
oblasti a ukázat na nich několik obecných postupů užitečných při návrhu
aproximačních algoritmů.
- Přibližná dualita [12,14]
- pro součtové toky [8]
- pro souběžné toky [13,2]
- Algoritmy na výpočet toků více komodit
- Metoda generovaní sloupců [4, kapitola 3.6]
- Lagrangeova relaxace a hladový algoritmus [6,7]
- Maximální řez a semidefinitní programování [9]
- Nejřidší řez (
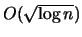 -aproximace, použití) [1]
-aproximace, použití) [1]
- Hledání hranově disjunktních cest a pakovací problémy [10]
- Toky krátkými cestami [11,3]
- 1
- S. Arora, S. Rao, and U. Vazirani.
Expander flows, geometric embeddings, and graph partitionings.
Journal of the AMC, 56(2):5.1-5.37, 2009.
Preliminary version in Proc. of the 36th ACM Symposium on Theory of Computing,
2004.
- 2
- Y. Aumann and Y. Rabani.
An 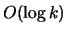 approximate min-cut max-flow theorem and
approximation algorithm.
approximate min-cut max-flow theorem and
approximation algorithm.
SIAM Journal on Computing, 27(1):291-301, 1998.
- 3
-
Baier, G., Erlebach, T., Hall, A., Köhler, E.,
Kolman P., Pangrác O., Schilling, H., and Skutella, M.
Length-bounded cuts and flows.
ACM Transactions on Algorithms, Volume 7, Issue 1, Article No. 4, 2010.
- 4
-
W. J. Cook, W. H. Cunningham, W. R. Pulleyblank, and A. Schrijver.
Combinatorial Optimization.
John Wiley, New York, 1997.
- 5
-
U. Feige and R. Krauthgamer.
A polylogarithmic approximation of the minimum bisection.
In Proc. of the 41st Annual Symposium on Foundations of Computer
Science, 105-115, 2000.
- 6
-
L. K. Fleischer.
Approximating fractional multicommodity flow independent of the
number of commodities.
SIAM Journal on Discrete Mathematics, 13(4):505-520, 2000.
- 7
-
N. Garg and J. Konemann.
Faster and simpler algorithms for multicommodity flow and other
fractional packing problems.
In Proc. of the 39th Annual Symposium on Foundations of Computer
Science, 300-309, 1998.
- 8
-
N. Garg, V. V. Vazirani, and M. Yannakakis.
Approximate max-flow min-cut theorems and their applications.
SIAM Journal on Computing, 25(2):235-251, Apr. 1996.
- 9
-
M. X. Goemans and D. P. Williamson.
.878-approximation algorithms for MAX CUT and MAX 2SAT.
In Proc. of the Twenty-Sixth Annual ACM Symposium on the
Theory of Computing, 422-431, 1994.
- 10
-
J. Kleinberg.
Approximation Algorithms for Disjoint Paths Problems.
PhD thesis, Department of Electrical Engineering and Computer
Science, Massachusetts Institute of Technology, 1996.
- 11
-
P. Kolman and C. Scheideler.
Improved bounds for the unsplittable flow problem.
In Proc. of the 13th ACM-SIAM Symposium on Discrete
Algorithms, 184-193, 2002.
- 12
-
T. Leighton and S. Rao.
An approximate max-flow min-cut theorem for uniform multicommodity
flow problems with applications to approximation algorithms.
In Proc. of the 29th Annual Symposium on Foundations of Computer
Science, 422-431, 1988.
- 13
-
N. Linial, E. London, and Y. Rabinovich.
The geometry of graphs and some of its algorithmic applications.
Combinatorica, 15:215-245, 1995.
- 14
-
D. B. Shmoys.
Cut problems and their application to divide-and-conquer.
In D. S. Hochbaum, editor, Approximation Algorithms for NP-hard
Problems, 192-235. PWS Publishing Company, 1997.
Petr Kolman
2009-09-29