Toky, cesty a řezy (DMI067)

Petr Kolman

Toky více komodit zobecňují přirozeným způsobem klasický tokový problém: místo jediné dvojice zdroj-spotřebič máme takových dvojic několik, ale přitom máme k dispozici stále jen jedinou siť, do které se musí všechny toky poskládat. Toky více komodit a zejména jejich duální řezové problémy hrály v posledním desetiletí významnou úlohu při návrhu aproximačních algoritmů pro celou radu rozmanitých aplikací. Cílem přednášky je představit vybrané výsledky z této oblasti a ukázat na nich několik obecných postupů užitečných při návrhu aproximačních algoritmů.

Předběžný program

• Algoritmy na výpočet toků více komodit
  • metoda generovaní sloupců [3, kapitola 3.6]
  • Lagrangeova relaxace a hladový algoritmus [5,6]
• Přibližná dualita [10]
  • pro součtové toky [7]
  • pro souběžné toky [11,2]
• Nejřidší řez ( 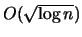$O(\sqrt{\log n})$-aproximace) a semidefinitní programování [1]
• Pouziti nejřidšího řezu
• Minimální rozpůlení [4] (možná preskocime)
• Hledání hranově disjunktních cest a pakovací problémy [8]
• Toky krátkými cestami [9]

Přednáska se koná 12:30 v S10.

Literatura

1

S. Arora, S. Rao, and U. Vazirani.
Expander flows, geometric embeddings, and graph partitionings.
In Proc. of the 36th ACM Symposium on Theory of Computing, 2004.

2

Y. Aumann and Y. Rabani.
An 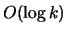$O(\log k)$ approximate min-cut max-flow theorem and approximation algorithm.
SIAM Journal on Computing, 27(1):291-301, 1998.

3

W. J. Cook, W. H. Cunningham, W. R. Pulleyblank, and A. Schrijver.
Combinatorial Optimization.
John Wiley, New York, 1997.

4

U. Feige and R. Krauthgamer.
A polylogarithmic approximation of the minimum bisection.
In Proceedings of the 41st Annual Symposium on Foundations of Computer Science, pages 105-115, 2000.

5

L. K. Fleischer.
Approximating fractional multicommodity flow independent of the number of commodities.
SIAM Journal on Discrete Mathematics, 13(4):505-520, 2000.

6

N. Garg and J. Konemann.
Faster and simpler algorithms for multicommodity flow and other fractional packing problems.
In 39th Annual Symposium on Foundations of Computer Science, pages 300-309, 1998.

7

N. Garg, V. V. Vazirani, and M. Yannakakis.
Approximate max-flow min-cut theorems and their applications.
SIAM Journal on Computing, 25(2):235-251, Apr. 1996.

8

J. Kleinberg.
Approximation Algorithms for Disjoint Paths Problems.
PhD thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 1996.

9

P. Kolman and C. Scheideler.
Improved bounds for the unsplittable flow problem.
In Proceedings of the 13th ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 184-193, 2002.

10

T. Leighton and S. Rao.
An approximate max-flow min-cut theorem for uniform multicommodity flow problems with applications to approximation algorithms.
In Proceedings of the 29th Annual Symposium on Foundations of Computer Science, pages 422-431, 1988.

11

N. Linial, E. London, and Y. Rabinovich.
The geometry of graphs and some of its algorithmic applications.
Combinatorica, 15:215-245, 1995.