The process of generating all 6-critical graphs has been split into three steps. We make available a program/programs to solve each of the three steps: generating all k-minimal graphs for k up to 10, generating all 2-cell embeddings of K6 in the Klein bottle, and finally generating 6-critical graphs from K6 by splitting vertices and gluing k-minimal graphs into faces. The details of the whole procedure can be found in our paper which is also available as a technical report of our department. Let us remark that we have independently written two sets of programs implementing all the three steps of the procedure. The programs available at this web-page were written by Bernard Lidicky in C++; the other set of programs was written by Dan Kral in C.
The programs write their output to stdout and information on the progress of computation to stderr. We describe the format of inputs and outputs of our programs in detail on this web-page. For some of the steps, the output of the previous step does not exactly match the input of the program in the next step, but it is easy to modify the output to the required form, e.g., using unix utility `sed'. It is always possible to download both inputs and outputs of our programs in the required form.
All source files, shell script, inputs and outputs for generating all 2-cell embeddings of 6-critical graphs on the Klein bottle can be downloaded as a tar.gz archive.
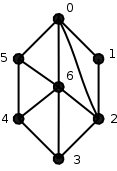
G:7 6 v: 7 0: 4 1 2 6 5 1: 2 0 2 2: 4 1 3 6 0 3: 3 6 2 4 4: 3 6 3 5 5: 3 6 4 0 6: 5 4 5 0 2 3
Each block of the above format describes a single minimal graph. The first line of the block starts with identifier `G:X' where X is replaced by a number identifying the graph starting with 0. Hence last number for k-critical graph is not the number of k-critical graphs but it is 2 less since we started from 0 and skipped the trivial one. The middle number on the first line is k for which the graph is k-minimal. The last number on the line (after v: ) determines the number of vertices. Each of the following lines of the block describe a single vertex: first, the number and the degree of the vertex are given (the vertices are numbered from 0), and they are followed by the neighbors of the vertex in the cyclic order around it. The 6-minimal graph corresponding to the block from the example can be found in the figure below.

Another program is used to convert the output of the previous program to the format similar to the final format of embeddings of K6 from the next step. A block representing a k-minimal graph starts with k followed by the number of vertices (v) and faces (f). Each of the following lines describe an inner face of the graph (its number, its size and the list of the vertices on its boundary in a cyclic order but not in some particular orientation); the outer faces is not explicitly described. Note that the outer face is always bounded by the cycle formed by the vertices 0, ..., k-1. Description of our 6-minimal example in the face format follows. Observe that the name of graph is not present there any more.
G:7 6 v: 7 f: 6 0: 3 2 0 1 1: 3 6 0 2 2: 3 5 0 6 3: 3 6 2 3 4: 3 4 3 6 5: 3 5 4 6
| Input | None |
| Output | list of k-minimal graphs |
| Source | k-minimal generator source |
| Input | list of k-minimal graphs |
| Output | k-minimal in face representation |
| Source | k-minimal to face representation source |
The outputs of the first two programs consist of lines of the following form:
0:12345 1:02354 2:04351 3:01524 4:03215 5:04132 00000 1100 001 01 0 G2X:12345 determines a cyclic order of neighbors around the vertex X (the vertices are numbered 0, 1, 2, 3, 4 and 5). The final part of the line then describe the ``orientation reversing'' matrix: 1 represents an edge flipping the orientation (passing through a cross-cap) and 0 an edge preserving the orientation. The matrix for the example line is:
.00000 0.1100 01.001 010.01 0000.0 00110.Each line ends with ``G2'' indicating that the Eulerian genus of the represented embedding is 2. The program can easily be modified to generate embeddings of a different genus.
The last of the three programs convert the output from the just described format to format where the embeddings are given as boundaries of the faces in the embedding (which is more suitable for manipulation in the remaining). The output of this program is comprised of blocks of the following form.
G:K6_X -1 v: 6 f: 9 F0: 4 0 1 4 2 F1: 4 0 1 2 5 F2: 4 0 2 1 3 F3: 3 0 3 4 F4: 3 0 4 5 F5: 3 1 3 5 F6: 3 1 4 5 F7: 3 2 3 5 F8: 3 2 3 4The first line of the block starts with a tag ``G:K6_X -1'' which should improve the readability of output (-1 should avoid confusion with embeddings of k-minimal graphs described in the previous section, X is replaced by a number indicating different embeddings of K6). The first line also contains the number of vertices (v - it is always 6) and the number of faces (f - it is always 9). The remaining lines describe the faces - the line starts with an identifier of the face, followed by the face length and the vertices on the boundary (the vertices are numbered starting from 0).
| Input | None |
| Output | K6 embeddings |
| Source | K6 generator source |
| Input | K6 embeddings |
| Output | non-isomorhic embedding of K6 |
| Source | K6 isomorfer source |
| Input | non-isomorphic embedding of K6 |
| Output | non-isomorhic embedding of K6 as faces |
| Source | K6 generator source |
There are two input files for this program. One contains all non-trivial k-minimal graphs for 4<=k<=10 and the other contains the list of all 2-cell embedding of K6 on the Klein bottle. The output of the program are all 2-cell non-isomorphic embeddings of 6-critical graphs on the Klein bottle (which can be obtained by reversing the reduction operation from the initial list of 6-critical graphs) and the list of all non-isomorphic 6-critical graphs. We argue in the paper that no new non-isomorphic embeddings can be obtained from the unique non-2-cell embeddings of K6 on the Klein bottle.
| Input | embeddings of K6, k-minimal graphs |
| Output | 6-critical graphs, drawings of 6-critical graphs |
| Source | splitter and gluer |
Table with number of k-minimal graphs including the trivial ones. The program does not generate the trivial ones and the graphs are numbered from zero. Thus the largest graph ID for k-minimal graphs is smaller by 2.
| k | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| # | 1 | 2 | 4 | 14 | 46 | 291 | 2124 | 19876 |
We found 190 2-cell embeddings of K6 on the Klein bottle but only 7 non-isomorphic.
And the result of gluing is 18 non-isomorphic 2-cell embeddings of 6-critical graphs on the projective plane and 9 non-isomorphic 6-critical graphs. Note that there is also one more embedding of K6 from the projective plane and it is not 2-cell (it is the unique embedding on the projective plane).